Bohm's Alternative to Quantum Mechanics

Blogger Ref http://www.p2pfoundation.net/Multi-Dimensional_Science



 David Albert Scientific American May 94
Last Words of a Quantum Heretic John Horgan New Scientist 29 Feb 93
The keystone of Bohr's interpretation was the concept of complementarily, which held that wave-particle duality is a paradox that cannot be resolved. Bohr also ruled out the possibility that the probabilistic behaviour of quantum systems was actually the result of underlying deterministic mechanisms called hidden variables. Reality was unknowable because it was intrinsically indefinite, Bohr insisted.

Particles are always particles
In trying to explain Bohr's approach, Bohm became dissatisfied with it. "The whole idea of science so far has been to say that underlying the phenomenon is some reality which explains things," he explained. "It was not that Bohr denied reality, but he said quantum mechanics implied there was nothing more that could be said about it." Such a view, Bohm decided, reduced quantum mechanics to "a system of formulas that we use to make predictions or to control things technologically. I said, that's not enough. I don't think I would be very interested in science if that were afl there was." In 1952 Bohm defied Bohr's prohibition against hidden-variable explanations in a classic two-part paper in Physical Review entitled "A suggested interpretation of the quantum theory in terms of 'hidden' variables". He proposed that particles are indeed particles-and at afl times, not just when they are observed. Their behaviour is determined by an unusual field or wave consisting both of classical versions of forces such as electromagnetism and an entirely new force-which Bohm called the quantum potential-that is responsible for nonclassical effects. The positions of particles in tum serve as the hidden variables determining the nature of the pilot wave. Bohm's interpretation was causal, or deterministic. Particles always had a distinct position and velocity, but any effort to measure these properties precisely would destroy information about them by physically altering the pilot wave. Bohm gave the uncertainty principle a purely physical rather than metaphysical meaning. Bohr had interpreted the uncertainty pn'nciple, Bohm explained, as meaning "not that there is uncertainty, but that there is an inherent ambiguity" in a quantum sv'tem. Bohm sent out preprints of the paper and was quickly informed that his interpretation was an old one, proposed 25 years earlier by Louis de Broglie. De Broglie had abandoned the pilot-wave concept after Wolfgang Pauli pointed out that, when applied to systems involving more than one particle, it led to "some very strange behaviour" This strange behaviour referred to by Pauli, Bohm realised, was nonlocality. Actually, nonlocality was a feature intrinsic to all quantum theories, not just Bohm's. Einstein had demonstrated this fact back in 1935 in an effort to show that quantum mechanics must be flawed. Working together with Boris Podolsky and Nathan Rosen at Princeton, Einstein proposed a thought experiment involving rwo particles that spring from a common source and fly in opposite directions. According to the standard model of quantum mechanics, neither particle has a definite position or momentum before it is measured; but by measuring the momentum of one particle, the physicist instantaneously forces the other particle to assume a fixed position-even if it is on the other side of the Galaxy. Deriding this effect as "spooky action at a distance", Einstein argued that it violated both common sense and the theory of relativity, which prohibits the propagation of effects faster than the speed of light-I quantum mechanics must be an incomplete theory. Perhaps because he had always had a holistic view of reality, Bohm was not disturbed by nonlocality. "I must have tacitly been feeling all along that quantum mechanics was nonlocal," he said. In Quantum Theory, Bohm even suggested an experiment that could demonstrate nonlocaliry more clearly and easily than the one proposed by Einstein, Podoisky and Rosen. Bohm called for measuring not the momentum and position of rwo particles from a common source but rather their spin. Bohm's spin experiment became the basis for a brilliant mathematical proof bv Bell in 1964 showing that no local hidden-variable theory could replicate the predictions of quantum mechanics. In 1982, a group led bN, the French physicist Alain Aspect at the University of Paris-South, carried out Bohm's experiment, demonstrating once and for all that quantum mechanics does indeed require spooky action. (The reason that nonlocality does not violate the theory of relativity is that one cannot exploit it to transmit infon-nation faster than light or instantaneously.) Bohm said he never had any doubts about the outcome of the experiment: 'it would have been a terrific surprise to find out otherwise." Ironically, Bell's theorem and the Aspect experiment were widely thought to rule out all hidden-variable theories, including Bohm's. It was Bell who pointed out years later that Bohm's theory, since it was nonlocal, was not ruled out by his theorem. According to Bohm's model, nonlocality was mediated through the pilot wave: any localised physical act, such as the measurement of a particle, would instantaneously alter the shape of the entire pilot wave, affecting all particles under its influence. Bohm continued to develop the pilot-wave theory through the 1980s with the help of collaborators such as Hiley. In its latest version, the Bohmian pilot wave is quite distinct from the one posited by de Broglie. De Broglie conceived of the pilot wave as a kind of mechanical force which pushed particles this way and that through the transmission of energy. Bohm's pilot wave is more subtle: it guides particles not through its amplitude but through its form-much as the form rather than the amplitude of a flight-controller's radio transmission controls a plane's behaviour. The wave's abuity to influence particles therefore does not diminish with distance, as classical waves do. In the last decade, Bohm also became absorbed in another perennial puzzle: why quantum effects are generally lim ited to very small-scale phenomena. Two recent efforts to explain this mystery left him unimpressed. One of these, proposed by Gian Carlo Ghirardi of the University of Trieste and others, holds that as a quantum entity propagates through space, its multiple, possible states converge into a single state that behaves in a classical way. Roger Penrose of the University of Oxford presented another possibility in his book The Emperor's New Mind: quantum effects disappear in systems containing so much mass that gravity-which is usually negligible at subatomic scales-becomes a factor. Bohm favoured what he felt was a much simpler explanation: heat. Various lines of evidence-notably the fact that superconductivity, which relies on quantum effects, occurs only at very low temperatures-suggest that thermal energy swamps quantum effects. To completely resolve the issue of the limits of quantum effects, Bohm contended that: "It would be required to connect thermodynamics and quantum mechanics in a deep ftindamental way rather than the present superficial way, which is that you start with quantum mechanics and then apply statistics. It may be that thermal properties are just as essential as quantum properties, or there's something deeper than both." To arrive at such a theory, physicists might need to jettison some basic assumptions about the organisation of nature. "Fundamental notions like order and structure condition our thinking unconsciously, and new kinds of theories depend on new kinds of order," he said. During the Enlightenment, he noted, thinkers such as Rene Descartes and Isaac Newton replaced the ancients' concept of order with a mechanistic view. Although the advent of relativity and other theories has brought about modifications in this order, Bohm said, "the basic idea is still the same: a mechanical order described by coordinates". Bohm himself began formulating what he called the implicate order several decades ago. His ideas were inspired in part by a simple experiment he saw on television, in which a drop of ink was squeezed onto a cylinder of glycerine. When the cylinder rotated, the ink diffused through the glycerine in an apparently irreversible fashion; its order seemed to have disintegrated. But when the direction of rotation was reversed, the ink gathered into a drop again. Bohm made this simple experiment into a metaphor for au of reality. Underlying the apparently chaotic realm of physical appearances-the explicate order-there is always a deeper, implicate order that is often hidden. Applying this concept to the quantum realm, Bohm proposed that the implicate order is the quantum potential, a field consisting of an infinite number of fluctuating waves. The overlapping of these waves generates what appear to us as particles: these constitute the explicate order. Even such seemingly fundamental conceprs as space and time may be merely explicate manifestations of some "nonlocal, deeper implicate order', according to Bohm. Bohm hoped the implicate order could even point the way to a resolution of that perennial conundrum of philosophy, the mind-matter problem. His belief was based on hints and rough analogies rather than on any concrete evidence. For example, he compared the way a pilot wave guides a particle to the way thought guides Ehe movements of a dancer. "The movement of the body is coming from thought, and the movement of the eleciron Ls coming from something very subtle, this wave. So there are similarities, which should make it possible to relate them."

Krishnamurti and David Bohm discuss the observer and the observed.

Despite his own enormous ambition as a truth seeker, Bohm rejected the possibility that scientists can ever bring their enterprise to an end by reducing all of nature to a single ftindamental phenomenon (such as infinitesimal particles called superstrings). "At each level we have something which is taken as appearance and something else is taken as the essence which explains the appearance. But there's no end to this. What underlies it all is unknown and cannot be grasped by thought." Indeed, scientists' belief that they are on the verge of a final theory may prevent them from seeking deeper truths. "It's like fish," Bohm elaborated. "If you have fish in a tank and you put a glass barrier in there, the fish learn to keep away from it. Then if you take the barrier away the fish never cross the barrier." Scientists who are frustrated at the thought that ultimate truths are unat tainable should consider the altemative. "They are going to be very frustrated if they get the final answer and then have nothing to do except be technicians," Bohm said. Science, Bohm believed, is sure to evolve in totally unexpected ways. He expressed the hope, for example, that future scientists wdl be less dependent on mathematics for modelling reality and will draw on new sources of metaphor and analogy. "We have an assumption now thaes getting stronger and stronger that mathematics is the only way to deal with reality," Bohm said. "Because it's worked so weLl for a while we've assumed that it has to be that way." Indeed, like some other scientific visionaries, Bohm expected that science and art would someday merge. "This division of art and science is temporary," he said. "It didn't exist in the past, and there's no reason why it should go on in the future." Just as art consists not simply of works of art but of an "attitude, the artistic spirit", so does science consist not in the accumulation of knowledge but in the creation of fresh modes of perception. 'The ability to perceive or think differently is more important than the knowledge gained." No matter how history treats Bohm's specific ideas, this, surely, wOl be one of his greatest legacies: his ability to make the rest of us perceive and think differently.
John Horgan

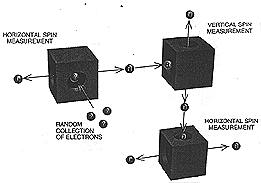
Spin behaviour is disrupted in a sequence ofthree measurementsElectrons are measured one at a time for their hrizontal spins (left), then for their vertical spins (right) and again for their horizontal spins (bottom). The vertical box disrupts the spin of half those electrons, so that half emerge from the second horizontal box with right spin and half with left.

Spin equivalent of two-slit interference: Two-path spin detection experiment depicts the unusual spin behaviour of electrons. On the left diagram right-spinning electrons are reflected back from an up down detector and recohered. The subsequent horizontal detector confirms they are all right spinning. However if one of the paths (top) are obstructed, then only 50% of the electrons subsequently measure as right spinning. This is because those which make it to the end definitely were down spinning and hence had had a disrupting measurement made of their vertical spin.

Bohm's theory can fully account for the outcomes of the experiments with the contraption-the experiment seemed to imply that electrons can be in states in which there fails to be any fact about where they are. in the case of an initially right-spinning electron fed into the apparatus, Bohm's theory entails that the electron wdl take either the up or the down route, period. Which of those two routes it takes wiu be fully determined by the particle's initial conditions, more specifically by its initial wave flmction and its initial position. Of course, certain details of those conditions wiu prove ixnpossible, as a matter of law, to ascertain by measurement. But the crucial point here is that whichever route the electron happens to take, its wave ftmction wiu split UP and take both. It wfll do so in accoidance with the linear differential equations of motion So, in the event that the electron jn question takes, say, the UP route, it wm nonetheless be reunited at the black box with the part of fts wave function that took the down route. How the down-route part of the wave function ends up pushing the electron around once the two are reunited wgl depend on the physical conditions encountered along the down path. To put ft a bit more suggestively, once the two parts of the electroifs wave fimction are reunited, the part that took the route that the electron itself did not take can inform the electron of what things were like along the way. For example, if a wall is inserted in the down route, the down component of the wave function will be missing at the exit of the black box. This absence in itself can constitute decisive information. Thus, the motion that such an electron executes, even if it took the up path through the apparatus, can depend quite dramaticaUy on whether or not such a wall was inserted. Moreover, Bohin's theory entails that the 'empty' part of the wave functionthe part that travels along the route the electron itself does not take-is completely undetectable. One of the consequences of the second equation in the box below is that only the part of any given particle's wave ftmction that is tly occupied by the particle itself can have any effect on the motions of other particles. So the empty part of the wave function-notwithstanding the fact that it is really, physically, thereis completely incapable of leaving any obsle trace of itself on detectors or anything else.
Hence, Bohm's theory accounts for all the unfathomable-looking behaviors of electrons discussed earlier every bit as well as the standard interpretation does. Moreover, and this point is important, ft is free of any of the metaphysical perplexties associated with quantum-mechanical -perposition.

Left: A graphical depiction of the quantum potential.
Right: Trajectories of an electron in a double slit experiment.

Bohm's theory-in Its entirety consists of three elements.
The first is a deterministic law (namely, Schödinger's equation) that describes how the wave functions of physical systems evolve over time. lt is:

where i is the imaginary number , h is Planck's constant, V is the wave function, H is a mathematical object called the Hamiltonian operator, N is the number of particles in the system, xl...X3N represent the spatial coordinates of those particles, and t is the time. Loosely speaking, the Hamiltonian operator describes the energy in the system.
The second element is a deterministic law of the motions of the particles:

where X1 ... X3N represent the actual coordinate values of the particles, dXj(t)/dt is the rate of change of X, at time t, and j represents the components of the standard quantum-mechanical probability current. The subscript i ranges from 1 to 3N.
The third element Is a statistical rule analogous to one used In classical statistical mechanics. It stipulates precisely how one goes about 'averaging over' one's Inevitable Ignorance of the exact states of physical systems. It runs as follows. Assume one is given the wave function of a certain system but no information about the positions of its particles. To calculate the motions of those particles in the future, what one ought to suppose is that the probability that those particles are currently located at some position (X1 ... X3N) is equal to . If information about the positions of the particles becomes available (as during a measurement), the rule indicates that that information ought to be used to 'update' the probabilities through a mathematical procedure called straightforward conditionalization. That is literally all there is to Bohm's theory. Whatever else we know about it derives strictly from these three elements.