Blogger Reference Link http://www.p2pfoundation.net/Multi-Dimensional_Science
From Wikipedia, the free encyclopedia
From Wikipedia, the free encyclopedia
(Redirected from Dimensions)
- Not to be confused with Dimension of a physical quantity. For other uses, see Dimension (disambiguation).
In physical terms, dimension refers to the constituent structure of all space (cf. volume) and its position in time (perceived as a scalar dimension along the t-axis), as well as the spatial constitution of objects within—structures that correlate with both particle and field conceptions, interact according to relative properties of mass—and are fundamentally mathematical in description. These, or other axes, may be referenced to uniquely identify a point or structure in its attitude and relationship to other objects and occurrences. Physical theories that incorporate time, such as general relativity, are said to work in 4-dimensional "spacetime", (defined as a Minkowski space). Modern theories tend to be "higher-dimensional" including quantum field and string theories. The state-space of quantum mechanics is an infinite-dimensional function space.
The concept of dimension is not restricted to physical objects. High-dimensional spaces occur in mathematics and the sciences for many reasons, frequently as configuration spaces such as in Lagrangian or Hamiltonian mechanics; these are abstract spaces, independent of the physical space we live in.
Contents[hide] |
[edit] In mathematics
In mathematics, the dimension of an object is an intrinsic property independent of the space in which the object is embedded. For example, a point on the unit circle in the plane can be specified by two Cartesian coordinates, but one can make do with a single coordinate (the polar coordinate angle), so the circle is 1-dimensional even though it exists in the 2-dimensional plane. This intrinsic notion of dimension is one of the chief ways the mathematical notion of dimension differs from its common usages.The dimension of Euclidean n-space En is n. When trying to generalize to other types of spaces, one is faced with the question “what makes En n-dimensional?" One answer is that to cover a fixed ball in En by small balls of radius ε, one needs on the order of ε-n such small balls. This observation leads to the definition of the Minkowski dimension and its more sophisticated variant, the Hausdorff dimension, but there are also other answers to that question. For example, one may observe that the boundary of a ball in En looks locally like En-1 and this leads to the notion of the inductive dimension. While these notions agree on En , they turn out to be different when one looks at more general spaces.
A tesseract is an example of a four-dimensional object. Whereas outside of mathematics the use of the term "dimension" is as in: "A tesseract has four dimensions", mathematicians usually express this as: "The tesseract has dimension 4", or: "The dimension of the tesseract is 4".
Although the notion of higher dimensions goes back to René Descartes, substantial development of a higher-dimensional geometry only began in the 19th century, via the work of Arthur Cayley, William Rowan Hamilton, Ludwig Schläfli and Bernhard Riemann. Riemann's 1854 Habilitationsschrift, Schlafi's 1852 Theorie der vielfachen Kontinuität, Hamilton's 1843 discovery of the quaternions and the construction of the Cayley Algebra marked the beginning of higher-dimensional geometry.
The rest of this section examines some of the more important mathematical definitions of the dimensions.
[edit] Dimension of a vector space
Main article: Dimension (vector space)
The dimension of a vector space is the number of vectors in any basis for the space, i.e. the number of coordinates necessary to specify any vector. This notion of dimension (the cardinality of a basis) is often referred to as the Hamel dimension or algebraic dimension to distinguish it from other notions of dimension.[edit] Manifolds
A connected topological manifold is locally homeomorphic to Euclidean n-space, and the number n is called the manifold's dimension. One can show that this yields a uniquely defined dimension for every connected topological manifold.For connected differential manifolds the dimension is also the dimension of the tangent vector space at any point
The theory of manifolds, in the field of geometric topology, is characterized by the way dimensions 1 and 2 are relatively elementary, the high-dimensional cases n > 4 are simplified by having extra space in which to "work"; and the cases n = 3 and 4 are in some senses the most difficult. This state of affairs was highly marked in the various cases of the Poincaré conjecture, where four different proof methods are applied.
[edit] Varieties
Main article: Dimension of an algebraic variety
The dimension of an algebraic variety may be defined in various equivalent ways. The most intuitive way is probably the dimension of the tangent space at any regular point.An algebraic set being a finite union of algebraic varieties, it dimension is the maximum of the dimensions of its components. It is equal to the maximal length of the chains
of sub varieties (the length of such a chain is the number of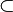 
.[edit] Krull dimension
Main article: Krull dimension
The Krull dimension of a commutative ring is the maximal length of prime ideals in it. It strongly related to the dimension of an algebraic variety, because of a natural correspondence between sub varieties and prime ideals of ring of the polynomials on the variety.For an algebra over a field, the dimension as vector space is finite if and only if its Krull dimension is 0.
[edit] Lebesgue covering dimension
Main article: Lebesgue covering dimension
For any normal topological space X, the Lebesgue covering dimension of X is defined to be n if n is the smallest integer for which the following holds: any open cover has an open refinement (a second open cover where each element is a subset of an element in the first cover) such that no point is included in more than n + 1 elements. In this case dim X = n. For X a manifold, this coincides with the dimension mentioned above. If no such integer n exists, then the dimension of X is said to be infinite, and one writes dim X = ∞. Moreover, X has dimension −1, i.e. dim X = −1 if and only if X is empty. This definition of covering dimension can be extended from the class of normal spaces to all Tychonoff spaces merely by replacing the term "open" in the definition by the term "functionally open".[edit] Inductive dimension
Main article: Inductive dimension
An inductive definition of dimension can be created as follows. Consider a discrete set of points (such as a finite collection of points) to be 0-dimensional. By dragging a 0-dimensional object in some direction, one obtains a 1-dimensional object. By dragging a 1-dimensional object in a new direction, one obtains a 2-dimensional object. In general one obtains an (n + 1)-dimensional object by dragging an n dimensional object in a new direction.The inductive dimension of a topological space may refer to the small inductive dimension or the large inductive dimension, and is based on the analogy that (n + 1)-dimensional balls have n dimensional boundaries, permitting an inductive definition based on the dimension of the boundaries of open sets.
[edit] Hausdorff dimension
Main article: Hausdorff dimension
For structurally complicated sets, especially fractals, the Hausdorff dimension is useful. The Hausdorff dimension is defined for all metric spaces and, unlike the Hamel dimension, can also attain non-integer real values.[3] The box dimension or Minkowski dimension is a variant of the same idea. In general, there exist more definitions of fractal dimensions that work for highly irregular sets and attain non-integer positive real values. Fractals have been found useful to describe many natural objects and phenomena.[4][5][edit] Hilbert spaces
Every Hilbert space admits an orthonormal basis, and any two such bases for a particular space have the same cardinality. This cardinality is called the dimension of the Hilbert space. This dimension is finite if and only if the space's Hamel dimension is finite, and in this case the above dimensions coincide.[edit] In physics
[edit] Spatial dimensions
Classical physics theories describe three physical dimensions: from a particular point in space, the basic directions in which we can move are up/down, left/right, and forward/backward. Movement in any other direction can be expressed in terms of just these three. Moving down is the same as moving up a negative distance. Moving diagonally upward and forward is just as the name of the direction implies; i.e., moving in a linear combination of up and forward. In its simplest form: a line describes one dimension, a plane describes two dimensions, and a cube describes three dimensions. (See Space and Cartesian coordinate system.)| Number of dimensions | Example co-ordinate systems | |||
|---|---|---|---|---|
| 1 |
| |||
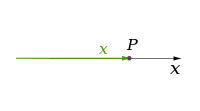
| 2 |
| |||
| 3 |
|
.svg&page=1)
[edit] Time
A temporal dimension is a dimension of time. Time is often referred to as the "fourth dimension" for this reason, but that is not to imply that it is a spatial dimension. A temporal dimension is one way to measure physical change. It is perceived differently from the three spatial dimensions in that there is only one of it, and that we cannot move freely in time but subjectively move in one direction.The equations used in physics to model reality do not treat time in the same way that humans commonly perceive it. The equations of classical mechanics are symmetric with respect to time, and equations of quantum mechanics are typically symmetric if both time and other quantities (such as charge and parity) are reversed. In these models, the perception of time flowing in one direction is an artifact of the laws of thermodynamics (we perceive time as flowing in the direction of increasing entropy).
The best-known treatment of time as a dimension is Poincaré and Einstein's special relativity (and extended to general relativity), which treats perceived space and time as components of a four-dimensional manifold, known as spacetime, and in the special, flat case as Minkowski space.
[edit] Additional dimensions
In physics, three dimensions of space and one of time is the accepted norm. There are theories that try to unify different forces and such—these theories require more dimensions. Superstring theory, M-theory and Bosonic string theory respectively posit that physical space has 10, 11 and 26 dimensions. These extra dimensions are said to be spatial. However, we perceive only three spatial dimensions and, to date, no experimental or observational evidence is available to confirm the existence of these extra dimensions. A possible explanation that has been suggested is that space acts as if it were "curled up" in the extra dimensions on a subatomic scale, possibly at the quark/string level of scale or below.An analysis of results from the Large Hadron Collider in December 2010 severely constrains theories with large extra dimensions.[6]
[edit] Networks and dimension
Some complex networks are characterized by fractal dimensions.[7] The concept of dimension can be generalized to include networks embedded in space.[8] The dimension characterize their spatial constraints.[edit] Literature
Perhaps the most basic way the word dimension is used in literature is as a hyperbolic synonym for feature, attribute, aspect, or magnitude. Frequently the hyperbole is quite literal as in he's so 2-dimensional, meaning that one can see at a glance what he is. This contrasts with 3-dimensional objects, which have an interior that is hidden from view, and a back that can only be seen with further examination.Science fiction texts often mention the concept of dimension, when really referring to parallel universes, alternate universes, or other planes of existence. This usage is derived from the idea that to travel to parallel/alternate universes/planes of existence one must travel in a direction/dimension besides the standard ones. In effect, the other universes/planes are just a small distance away from our own, but the distance is in a fourth (or higher) spatial (or non-spatial) dimension, not the standard ones.
One of the most heralded science fiction novellas regarding true geometric dimensionality, and often recommended as a starting point for those just starting to investigate such matters, is the 1884 novel Flatland by Edwin A. Abbott. Isaac Asimov, in his foreword to the Signet Classics 1984 edition, described Flatland as "The best introduction one can find into the manner of perceiving dimensions."
The idea of other dimensions was incorporated into many early science fiction stories, appearing prominently, for example, in Miles J. Breuer's The Appendix and the Spectacles (1928) and Murray Leinster's The Fifth-Dimension Catapult (1931); and appeared irregularly in science fiction by the 1940s. Some of the classic stories involving other dimensions include Robert A. Heinlein's 1941 —And He Built a Crooked House, in which a California architect designs a house based on a three-dimensional projection of a tesseract, and Alan E. Nourse's Tiger by the Tail and The Universe Between, both from 1951. Another reference is Madeleine L'Engle's novel A Wrinkle In Time (1962), which uses the 5th Dimension as a way for "tesseracting the universe" or in a better sense, "folding" space in half to move across it quickly. The fourth and fifth dimensions were also a key component of the book The Boy Who Reversed Himself, by William Sleator.
[edit] Philosophy
In 1783, Kant wrote: "That everywhere space (which is not itself the boundary of another space) has three dimensions and that space in general cannot have more dimensions is based on the proposition that not more than three lines can intersect at right angles in one point. This proposition cannot at all be shown from concepts, but rests immediately on intuition and indeed on pure intuition a priori because it is apodictically (demonstrably) certain."[9][edit] More dimensions
- Degrees of freedom (mechanics)
- Degrees of freedom (physics and chemistry)
- Degrees of freedom (statistics)
- Dimension of an algebraic variety
- Exterior dimension
- Hurst exponent
- Isoperimetric dimension
- Kaplan–Yorke dimension
- Lebesgue covering dimension
- Lyapunov dimension
- Metric dimension
- Pointwise dimension
- Poset dimension
- q-dimension; especially:
- Information dimension (corresponding to q = 1)
- Correlation dimension (corresponding to q = 2)
- Vector space dimension / Hamel dimension
[edit] See also
- Dimension (data warehouse) and dimension tables
- Dimensional analysis
- Fractal dimension
- Hyperspace (disambiguation page)
- Space-filling curve
- Intrinsic dimension
- Demonstrating Size (dimension)
[edit] A list of topics indexed by dimension
- Zero dimensions:
- One dimension:
- Line
- Graph (combinatorics)
- Real number
- Two dimensions:
- Three dimensions
- Platonic solid
- Stereoscopy (3-D imaging)
- Euler angles
- 3-manifold
- Knot (mathematics)
- Four dimensions:
- High-dimensional topics from mathematics:
- High-dimensional topics from physics:
- Infinitely many dimensions:
[edit] References
 | This article needs additional citations for verification. (May 2010) |
- ^ Curious About Astronomy
- ^ MathWorld: Dimension
- ^ Fractal Dimension, Boston University Department of Mathematics and Statistics
- ^ S. Havlin, A. Bunde (1991). Fractals and Disordered Systems. Springer. http://havlin.biu.ac.il/Shlomo%20Havlin%20books_fds.php.
- ^ S. Havlin, A. Bunde (1994). Fractals in Science. Springer. http://havlin.biu.ac.il/Shlomo%20Havlin%20books_fds.php.
- ^ CMS Collaoration, "Search for Microscopic Black Hole Signatures at the Large Hadron Collider," http://arxiv.org/abs/1012.3375
- ^ C.M. Song, S. Havlin, H.A. Makse (2005). "Self-similarity of complex networks". Nature 433: 7024. arXiv:cond-mat/0503078v1. Bibcode 2005Natur.433..392S. doi:10.1038/nature03248. http://havlin.biu.ac.il/Publications.php?keyword=Self-similarity+of+complex+networks&year=*&match=all.
- ^ D. Li, K. Kosmidis, A. Bunde, S. Havlin (2011). "Dimension of spatially embedded networks". Nature Physics. Bibcode 2011NatPh...7..481D. doi:10.1038/nphys1932. http://havlin.biu.ac.il/Publications.php?keyword=Dimension+of+spatially+embedded+networks&year=*&match=all.
- ^ Prolegomena, § 12
[edit] Further reading
- Edwin A. Abbott, (1884) Flatland: A Romance of Many Dimensions, Public Domain. Online version with ASCII approximation of illustrations at Project Gutenberg.
- Thomas Banchoff, (1996) Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions, Second Edition, Freeman.
- Clifford A. Pickover, (1999) Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons, Oxford University Press.
- Rudy Rucker, (1984) The Fourth Dimension, Houghton-Mifflin.
- Michio Kaku, (1994) Hyperspace, a Scientific Odyssey Through the 10th Dimension, Oxford University Press.
| |||||||||||||||||
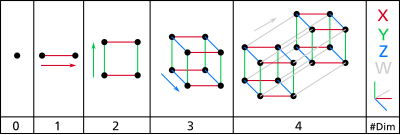
No comments:
Post a Comment