Fractals

From Wikipedia, the free encyclopedia

For other uses, see Fractal (disambiguation).

Listen to this article (info/dl)

This audio file was created from a revision of the "Fractal" article dated 2005-06-16, and does not reflect subsequent edits to the article. (Audio help)

More spoken articles

Figure 1a. The Mandelbrot set illustrates self-similarity. As you zoom in on the image at finer and finer scales, the same pattern re-appears so that it is virtually impossible to know at which level you are looking.

Figure 1b. Mandelbrot zoomed 6x

Figure 1c. Mandelbrot zoomed 100x

Figure 1d. Even 2000 times magnification of the Mandelbrot set uncovers fine detail resembling the full set.

A fractal is a mathematical set that has a fractal dimension that usually exceeds itstopological dimension^[1] and may fall between the integers.^[2] Fractals are typically self-similar patterns, where self-similar means they are "the same from near as from far".^[3]Fractals may be exactly the same at every scale, or, as illustrated in Figure 1, they may be nearly the same at different scales.^[2][4][5][6] The definition of fractal goes beyond self-similarity per se to exclude trivial self-similarity and include the idea of a detailed patternrepeating itself.^{[2]:166; 18[4][7]}

As mathematical equations, fractals are usually nowhere differentiable, which means that they cannot be measured in traditional ways.^[2][6][8] An infinite fractal curve can be perceived of as winding through space differently from an ordinary line, still being a 1-dimensional line yet having a fractal dimension indicating it also resembles a surface.^[1]:48[2]:15

The mathematical roots of the idea of fractals have been traced through a formal path of published works, starting in the 17th century with notions of recursion, then moving through increasingly rigorous mathematical treatment of the concept to the study of continuous but notdifferentiable functions in the 19th century, and on to the coining of the word fractal in the 20th century with a subsequent burgeoning of interest in fractals and computer-based modelling in the 21st century.^[9][10] The term "fractal" was first used by mathematician Benoît Mandelbrot in 1975. Mandelbrot based it on the Latin frāctus meaning "broken" or "fractured", and used it to extend the concept of theoretical fractional dimensions to geometric patterns in nature.^[2]:405[7]

There is some disagreement amongst authorities about how the concept of a fractal should be formally defined. The general consensus is that theoretical fractals are infinitely self-similar,iterated, and detailed mathematical constructs having fractal dimensions, of which manyexamples have been formulated and studied in great depth.^[2][4][5] Fractals are not limited to geometric patterns, but can also describe processes in time.^[3][6][11] Fractal patterns with various degrees of self-similarity have been rendered or studied in images, structures and sounds^[12] and found in nature,^{[13][14][15][16][17]} technology,^{[18][19][20][21]} art,^[22][23][24] and law.^[25]

Contents   [hide]  1 Introduction 2 History 3 Characteristics 4 Common techniques for generating fractals 5 Simulated fractals 6 Natural phenomena with fractal features 7 In creative works 8 In law 9 Applications in technology 10 See also 10.1 Fractal-generating programs 11 Notes 12 References 13 Further reading 14 External links

[edit]Introduction

The word "fractal" often has different connotations for laypeople than mathematicians, where the layperson is more likely to be familiar with fractal art than a mathematical conception. The mathematical concept is difficult to formally define even for mathematicians, but key features can be understood with little mathematical background.

The feature of "self-similarity", for instance, is easily understood by analogy to zooming in with a lens or other device that zooms in on digital images to uncover finer, previously invisible, new structure. If this is done on fractals, however, no new detail appears; nothing changes and the same pattern repeats over and over, or for some fractals, nearly the same pattern reappears over and over. Self-similarity itself is not necessarily counter-intuitive (e.g., people have pondered self-similarity informally such as in the infinite regress in parallel mirrors or the homunculus, the little man inside the head of the little man inside the head...). The difference for fractals is that the pattern reproduced must be detailed.^{[2]:166; 18[4][7]}

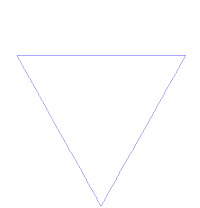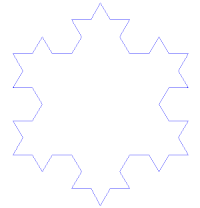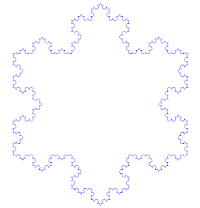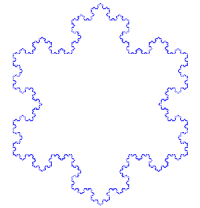
This idea of being detailed relates to another feature that can be understood without mathematical background: Having a fractional orfractal dimension greater than its topological dimension, for instance, refers to how a fractal scales compared to how geometric shapes are usually perceived. A regular line, for instance, is conventionally understood to be 1-dimensional; if such a curve is divided into pieces each 1/3 the length of the original, there are always 3 equal pieces. In contrast, consider the curve in Figure 2. It is also 1-dimensional for the same reason as the ordinary line, but it has, in addition, a fractal dimension greater than 1 because of how its detail can be measured. The fractal curve divided into parts 1/3 the length of the original line becomes 4 pieces rearranged to repeat the original detail, and this unusual relationship is the basis of its fractal dimension.

This also leads to understanding a third feature, that fractals as mathematical equations are "nowhere differentiable". In a concrete sense, this means fractals cannot be measured in traditional ways.^[2][6][8] To elaborate, in trying to find the length of a wavy non-fractal curve, one could find straight segments of some measuring tool small enough to lay end to end over the waves, where the pieces could get small enough to be considered to conform to the curve in the normal manner of measuring with a tape measure. But in measuring a wavy fractal curve such as the one in Figure 2, one would never find a small enough straight segment to conform to the curve, because the wavy pattern would always re-appear, albeit at a smaller size, essentially pulling a little more of the tape measure into the total length measured each time one attempted to fit it tighter and tighter to the curve. This is perhaps counter-intuitive, but it is how fractals behave.^[2]

[edit]History

Figure 2. Koch snowflake, a fractal that begins with an equilateral triangle and then replaces the middle third of every line segment with a pair of line segments that form an equilateral "bump"

The history of fractals traces a path from chiefly theoretical studies to modern applications in computer graphics, with several notable people contributing canonical fractal forms along the way.^[9][10] According to Pickover, the mathematics behind fractals began to take shape in the 17th century when the mathematician and philosopher Gottfried Leibniz pondered recursive self-similarity (although he made the mistake of thinking that only the straight line was self-similar in this sense).^[26] In his writings, Leibniz used the term "fractional exponents", but lamented that "Geometry" did not yet know of them^[2]:405. Indeed, according to various historical accounts, after that point few mathematicians tackled the issues and the work of those who did remained obscured largely because of resistance to such unfamiliar emerging concepts, which were sometimes referred to as mathematical "monsters".^[8][9][10] Thus, it was not until two centuries had passed that in 1872 Karl Weierstrass presented the first definition of a function with a graphthat would today be considered fractal, having the non-intuitive property of being everywherecontinuous but nowhere differentiable.^[9]:7[10] Not long after that, in 1883, Georg Cantor, who attended lectures by Weierstrass,^[10] published examples of subsets of the real line known asCantor sets, which had unusual properties and are now recognized as fractals.^[9]:11-24 Also in the last part of that century, Felix Klein and Henri Poincaré introduced a category of fractal that has come to be called "self-inverse" fractals.^[2]:166

Figure 3. A Julia set, a fractal related to the Mandelbrot set

One of the next milestones came in 1904, when Helge von Koch, extending ideas of Poincaré and dissatisfied with Weierstrass's abstract and analytic definition, gave a more geometric definition including hand drawn images of a similar function, which is now called the Koch curve(see Figure 2)^[9]:25.^[10] Another milestone came a decade later in 1915, when Wacław Sierpińskiconstructed his famous triangle then, one year later, his carpet. By 1918, two French mathematicians, Pierre Fatou and Gaston Julia, though working independently, arrived essentially simultaneously at results describing what are now seen as fractal behaviour associated with mapping complex numbers and iterative functions and leading to further ideas about attractors and repellors (i.e., points that attract or repel other points), which have become very important in the study of fractals (see Figure 3 and Figure 4).^[6][9][10] Very shortly after that work was submitted, by March 1918, Felix Hausdorff expanded the definition of "dimension", significantly for the evolution of the definition of fractals, to allow for sets to have noninteger dimensions.^[10] The idea of self-similar curves was taken further by Paul Pierre Lévy, who, in his 1938 paper Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole described a new fractal curve, the Lévy C curve.^{[notes 1]}

Figure 4. A strange attractor that exhibits multifractal scaling

Different researchers have postulated that without the aid of modern computer graphics, early investigators were limited to what they could depict in manual drawings, so lacked the means to visualize the beauty and appreciate some of the implications of many of the patterns they had discovered (the Julia set, for instance, could only be visualized through a few iterations as very simple drawings hardly resembling the image in Figure 3).^{[2]:179[8][10]} That changed, however, in the 1960s, when Benoît Mandelbrot started writing about self-similarity in papers such as How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension,^[27] which built on earlier work by Lewis Fry Richardson. In 1975^[7] Mandelbrot solidified hundreds of years of thought and mathematical development in coining the word "fractal" and illustrated his mathematical definition with striking computer-constructed visualizations. These images, such as of his canonical Mandelbrot set pictured in Figure 1 captured the popular imagination; many of them were based on recursion, leading to the popular meaning of the term "fractal".^[28]Currently, fractal studies are essentially exclusively computer-based.^[8][9][26]

[edit]Characteristics

One often cited description that Mandelbrot published to describe geometric fractals is "a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole";^[2] this is generally helpful but limited. Authorities disagree on the exact definition of fractal, but most usually elaborate on the basic ideas of self-similarity and an unusual relationship with the space a fractal is embedded in.^{[2][3][4] [6][29]} One point agreed on is that fractal patterns are characterized by fractal dimensions, but whereas these numbers quantify complexity (i.e., changing detail with changing scale), they neither uniquely describe nor specify details of how to construct particular fractal patterns.^[30] In 1975 when Mandelbrot coined the word "fractal", he did so to denote an object whose Hausdorff–Besicovitch dimension is greater than its topological dimension.^[7] It has been noted that this dimensional requirement is not met by fractal space-filling curves such as the Hilbert curve.^{[notes 2]}

According to Falconer, rather than being strictly defined, fractals should, in addition to being differentiable and able to have a fractal dimension, be generally characterized by a gestalt of the following features^[4]:

• Self-similarity, which may be manifested as:

• Exact self-similarity: identical at all scales; e.g. Koch snowflake
• Quasi self-similarity: approximates the same pattern at different scales; may contain small copies of the entire fractal in distorted and degenerate forms; e.g., the Mandelbrot set's satellites are approximations of the entire set, but not exact copies, as shown in Figure 1
• Statistical self-similarity: repeats a pattern stochastically so numerical or statistical measures are preserved across scales; e.g., randomly generated fractals; the well-known example of the coastline of Britain, for which one would not expect to find a segment scaled and repeated as neatly as the repeated unit that defines, for example, the Koch snowflake^[6]
• Qualitative self-similarity: as in a time series^[11]
• Multifractal scaling: characterized by more than one fractal dimension or scaling rule

• Fine or detailed structure at arbitrarily small scales. A consequence of this structure is fractals may have emergent properties^[31](related to the next criterion in this list).

• Irregularity locally and globally that is not easily described in traditional Euclidean geometric language. For images of fractal patterns, this has been expressed by phrases such as "smoothly piling up surfaces" and "swirls upon swirls".^[1]

• Simple and "perhaps recursive" definitions see Common techniques for generating fractals

As a group, these criteria form guidelines for excluding certain cases, such as those that may be self-similar without having other typically fractal features. A straight line, for instance, is self-similar but not fractal because it lacks detail, is easily described in Euclidean language, has the same Hausdorff dimension as topological dimension, and is fully defined without a need for recursion.^[2][6]

[edit]Common techniques for generating fractals

Figure 5. Self-similar branching pattern modeled in silico using L-systems principles^[17]

Images of fractals can be created by fractal generating programs.

• Iterated function systems – use fixed geometric replacement rules; may be stochastic or deterministic;^[32] e.g., Koch snowflake, Cantor set, Haferman carpet^[33], Sierpinski carpet, Sierpinski gasket, Peano curve, Harter-Heighway dragon curve, T-Square, Menger sponge

• Strange attractors – use iterations of a map or solutions of a system of initial-value differential equations that exhibit chaos (e.g., see multifractal image)

• L-systems - use string rewriting; may resemble branching patterns, such as in plants, biological cells (e.g., neurons and immune system cells^[17]), blood vessels, pulmonary structure,^[34] etc. (e.g., see Figure 5) or turtle graphics patterns such as space-filling curves and tilings

• Escape-time fractals – use a formula or recurrence relation at each point in a space (such as the complex plane); usually quasi-self-similar; also known as "orbit" fractals; e.g., the Mandelbrot set, Julia set, Burning Ship fractal, Nova fractal and Lyapunov fractal. The 2d vector fields that are generated by one or two iterations of escape-time formulae also give rise to a fractal form when points (or pixel data) are passed through this field repeatedly.

• Random fractals – use stochastic rules; e.g., Lévy flight, percolation clusters, self avoiding walks, fractal landscapes, trajectories of Brownian motion and the Brownian tree (i.e., dendritic fractals generated by modeling diffusion-limited aggregation or reaction-limited aggregation clusters).^[6]

[edit]Simulated fractals

A fractal flame

Fractal patterns have been modeled extensively, albeit within a range of scales rather than infinitely, owing to the practical limits of physical time and space. Models may simulate theoretical fractals or natural phenomena with fractal features. The outputs of the modelling process may be highly artistic renderings, outputs for investigation, or benchmarks for fractal analysis. Some specific applications of fractals to technology are listed elsewhere. Images and other outputs of modelling are normally referred to as being "fractals" even if they do not have strictly fractal characteristics, such as when it is possible to zoom into a region of the fractal image that does not exhibit any fractal properties. Also, these may include calculation or displayartifacts which are not characteristics of true fractals.

Modeled fractals may be sounds,^[12] digital images, electrochemical patterns, circadian rhythms,^[35] etc. Fractal patterns have been reconstructed in physical 3-dimensional space^[20]:10 and virtually, often called "in silico" modeling.^[34] Models of fractals are generally created using fractal-generating softwarethat implements techniques such as those outlined above.^[6][11][20] As one illustration, trees, ferns, cells of the nervous system,^[17]blood and lung vasculature,^[34] and other branching patterns in nature can be modeled on a computer by using recursive algorithms andL-systems techniques.^[17] The recursive nature of some patterns is obvious in certain examples—a branch from a tree or a frond from afern is a miniature replica of the whole: not identical, but similar in nature. Similarly, random fractals have been used to describe/create many highly irregular real-world objects. A limitation of modeling fractals is that resemblance of a fractal model to a natural phenomenon does not prove that the phenomenon being modeled is formed by a process similar to the modeling algorithm.

[edit]Natural phenomena with fractal features

Further information: Patterns in nature

Approximate fractals found in nature display self-similarity over extended, but finite, scale ranges. The connection between fractals and leaves, for instance, is currently being used to determine how much carbon is contained in trees.^[36]

Examples of phenomena known or anticipated to have fractal features are listed below:

clouds river networks fault lines mountain ranges      craters lightning bolts coastlines

animal coloration patterns       Romanesco broccoli heart rates[13] heartbeat[14] earthquakes[21][37] snow flakes[38]

crystals[39] blood vessels and pulmonary vessels[34] ocean waves[40] DNA various vegetables (cauliflower & broccoli) Psychological subjective perception[41]

Frost crystals formed naturally on cold glass illustrate fractal process development in a purely physical system   A fractal is formed when pulling apart two glue-covered acrylicsheets   High voltage breakdown within a 4″ block of acrylic creates a fractalLichtenberg figure   Romanesco broccoli, showingself-similar form approximating a natural fractal

[edit]In creative works

A fractal that models the surface of a mountain (animation)

Further information: Fractal art

Fractal patterns have been found in the paintings of American artist Jackson Pollock. While Pollock's paintings appear to be composed of chaotic dripping and splattering, computer analysis has found fractal patterns in his work.^[24]

Decalcomania, a technique used by artists such as Max Ernst, can produce fractal-like patterns.^[42] It involves pressing paint between two surfaces and pulling them apart.

Cyberneticist Ron Eglash has suggested that fractal geometry and mathematics are prevalent inAfrican art, games, divination, trade, and architecture. Circular houses appear in circles of circles, rectangular houses in rectangles of rectangles, and so on. Such scaling patterns can also be found in African textiles, sculpture, and even cornrow hairstyles.^[23][43] Following his research, Spanish architect Xavier Vilaltauses fractal geometry in contemporary architecture designs.

In a 1996 interview with Michael Silverblatt, David Foster Wallace admitted that the structure of the first draft of Infinite Jest he gave to his editor Michael Pietsch was inspired by fractals, specifically the Sierpinski triangle (aka Sierpinski gasket) but that the edited novel is "more like a lopsided Sierpinsky Gasket".^[22]

[edit]In law

If a rule or principle of law is conceptualized as defining a two-dimensional "area" of conduct, conduct within which should be legal and conduct outside of which should be illegal, it has been observed that the border of that area must be a fractal, because of the infinite and recursive potential exceptions and extensions necessary to account appropriately for all variations in fact pattern that may arise.^[25]

[edit]Applications in technology

Main article: Fractal analysis

fractal antennas[44] Fractal transistor[45] digital imaging urban growth[46][47] Classification of histopathology slides Fractal landscape or Coastline complexity Enzyme/enzymology (Michaelis-Menten kinetics) Generation of new music Signal and image compression Creation of digital photographic enlargements Seismology Fractal in soil mechanics

Computer and video game design computer graphics organic environments procedural generation Fractography and fracture mechanics Small angle scattering theory of fractally rough systems T-shirts and other fashion Generation of patterns for camouflage, such asMARPAT Digital sundial Technical analysis of price series Fractals in networks

medicine[20] neuroscience[15][16] diagnostic imaging[19] pathology[48][49] geology[50] geography[51] archaeology[52][53] soil mechanics[18] seismology[21] search and rescue[54] technical analysis[55]

[edit]See also

Banach fixed point theorem           Bifurcation theory Box counting Butterfly effect Complexity Constructal theory Cymatics Diamond-square algorithm Droste effect Feigenbaum function Fractal compression

Fractal cosmology Fractal-generating software Fracton Golden ratio Graftal Greeble Lacunarity List of fractals by Hausdorff dimension           Publications in fractal geometry Mandelbulb

Multifractal system Newton fractal Patterns in nature Percolation Power law Random walk Sacred geometry Self-reference Strange loop Turbulence

[edit]Fractal-generating programs

This section does not cite anyreferences or sources.(January 2012)

There are many fractal generating programs available, both free and commercial. Some of the fractal generating programs include:

• Apophysis - open source software for Microsoft Windows based systems
• Electric Sheep - open source distributed computing software
• Fractint - freeware with available source code
• Sterling - Freeware software for Microsoft Windows based systems
• SpangFract - For Mac OS
• Ultra Fractal - A proprietary fractal generator for Microsoft Windows and Mac OS X based systems
• XaoS - A cross platform open source fractal zooming program
• Terragen - a fractal terrain generator

Most of the above programs make two-dimensional fractals, with a few creating three-dimensional fractal objects, such as a Quaternion. A specific type of three-dimensional fractal, called mandelbulbs, was introduced in 2009.

[edit]Notes

1. ^ The original paper, Lévy, Paul (1938). "Les Courbes planes ou gauches et les surfaces composées de parties semblables au tout".Journal de l'École Polytechnique: 227–247, 249–291., is translated in Edgar, pages 181-239.
2. ^ The Hilbert curve map is not a homeomorphism, so it does not preserve topological dimension. The topological dimension and Hausdorff dimension of the image of the Hilbert map in R² are both 2. Note, however, that the topological dimension of the graph of the Hilbert map (a set in R³) is 1.

[edit]References

1. ^ ^a b c Mandelbrot, Benoît B. (2004). Fractals and Chaos. Berlin: Springer. p. 38. ISBN 978-0-387-20158-0. "A fractal set is one for which the fractal (Hausdorff-Besicovitch) dimension strictly exceeds the topological dimension"
2. ^ ^{a b c d e f g h i j k l m n o p} Mandelbrot, Benoît B. (1983). The fractal geometry of nature. Macmillan. ISBN 978-0-7167-1186-5. Retrieved 1 February 2012.
3. ^ ^a b c Gouyet, Jean-François (1996). Physics and fractal structures. Paris/New York: Masson Springer. ISBN 978-0-387-94153-0.
4. ^ ^{a b c d e f} Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Ltd.. xxv. ISBN 0-470-84862-6.
5. ^ ^a b Briggs, John (1992). Fractals:The Patterns of Chaos. London, UK: Thames and Hudson. p. 148. ISBN 0-500-27693-5, 0500276935.
6. ^ ^{a b c d e f g h i j} Vicsek, Tamás (1992). Fractal growth phenomena. Singapore/New Jersey: World Scientific. pp. 31; 139–146. ISBN 978-981-02-0668-0.
7. ^ ^{a b c d e} Albers, Donald J.; Alexanderson, Gerald L. (2008). "Benoît Mandelbrot: In his own words". Mathematical people : profiles and interviews. Wellesley, MA: AK Peters. p. 214.ISBN 978-1-56881-340-0.
8. ^ ^{a b c d e} Gordon, Nigel (2000). Introducing fractal geometry. Duxford, UK: Icon. p. 71. ISBN 978-1-84046-123-7.
9. ^ ^{a b c d e f g h} Edgar, Gerald (2004). Classics on Fractals. Boulder, CO: Westview Press. ISBN 978-0-8133-4153-8.
10. ^ ^{a b c d e f g h i} Trochet, Holly (2009). "A History of Fractal Geometry". MacTutor History of Mathematics. Archived from the original on 4 February 2012.
11. ^ ^a b c Peters, Edgar (1996). Chaos and order in the capital markets : a new view of cycles, prices, and market volatility. New York: Wiley. ISBN 0-471-13938-6.
12. ^ ^a b Brothers, Harlan J. (2007). "Structural Scaling in Bach's Cello Suite No. 3". Fractals 15: 89–95.doi:10.1142/S0218348X0700337X. edit
13. ^ ^a b Tan, Can Ozan; Cohen, Michael A.; Eckberg, Dwain L.; Taylor, J. Andrew (2009). "Fractal properties of human heart period variability: Physiological and methodological implications". The Journal of Physiology 587 (15): 3929.doi:10.1113/jphysiol.2009.169219. edit
14. ^ ^a b Buldyrev, Sergey V.; Goldberger, Ary L.; Havlin, Shlomo; Peng, Chung-Kang; Stanley, H. Eugene (1995). "3". In Bunde, Armin; Havlin, Shlomo. Fractals in Science. Springer.
15. ^ ^a b Liu, Jing Z.; Zhang, Lu D.; Yue, Guang H. (2003). "Fractal Dimension in Human Cerebellum Measured by Magnetic Resonance Imaging". Biophysical Journal 85 (6): 4041–4046.doi:10.1016/S0006-3495(03)74817-6. PMC 1303704.PMID 14645092. edit
16. ^ ^a b Karperien, Audrey L.; Jelinek, Herbert F.; Buchan, Alastair M. (2008). "Box-Counting Analysis of Microglia Form in Schizophrenia, Alzheimer's Disease and Affective Disorder".Fractals 16 (2): 103. doi:10.1142/S0218348X08003880. edit
17. ^ ^{a b c d e} Jelinek, Herbert F.; Karperien, Audrey; Cornforth, David; Cesar, Roberto; Leandro, Jorge de Jesus Gomes (2002). "MicroMod-an L-systems approach to neural modelling". In Sarker, Ruhul. Workshop proceedings: the Sixth Australia-Japan Joint Workshop on Intelligent and Evolutionary Systems, University House, ANU,. University of New South Wales. ISBN 9780731705054. OCLC 224846454.http://researchoutput.csu.edu.au/R/-?func=dbin-jump-full&object_id=6595&local_base=GEN01-CSU01. Retrieved 3 February 2012.
18. ^ ^a b Hu, Shougeng; Cheng, Qiuming; Wang, Le; Xie, Shuyun (2012). "Multifractal characterization of urban residential land price in space and time". Applied Geography 34: 161.doi:10.1016/j.apgeog.2011.10.016. edit
19. ^ ^a b Karperien, Audrey; Jelinek, Herbert F.; Leandro, Jorge de Jesus Gomes; Soares, João V. B.; Cesar Jr, Roberto M.; Luckie, Alan (2008). "Automated detection of proliferative retinopathy in clinical practice". Clinical ophthalmology (Auckland, N.Z.) 2(1): 109–122. doi:10.2147/OPTH.S1579. PMC 2698675.PMID 19668394. edit
20. ^ ^a b c d Losa, Gabriele A.; Nonnenmacher, Theo F. (2005).Fractals in biology and medicine. Springer. ISBN 978-3-7643-7172-2. Retrieved 1 February 2012.
21. ^ ^a b c Vannucchi, Paola; Leoni, Lorenzo (2007). "Structural characterization of the Costa Rica décollement: Evidence for seismically-induced fluid pulsing". Earth and Planetary Science Letters 262 (3–4): 413. Bibcode 2007E&PSL.262..413V.doi:10.1016/j.epsl.2007.07.056. edit
22. ^ ^a b Wallace, David Foster. "Bookworm on KCRW". Kcrw.com. Retrieved 2010-10-17.
23. ^ ^a b Eglash, Ron (1999). "African Fractals: Modern Computing and Indigenous Design". New Brunswick: Rutgers University Press. Retrieved 2010-10-17.
24. ^ ^a b Taylor, Richard; Micolich, Adam P.; Jonas, David. "Fractal Expressionism: Can Science Be Used To Further Our Understanding Of Art?". Phys.unsw.edu.au. Retrieved 2010-10-17.
25. ^ ^a b Stumpff, Andrew. "The Law is a Fractal: The Attempt to Anticipate Everything". Loyola University Chicago Law Journal. Retrieved 2012-10-5.
26. ^ ^a b Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. Sterling Publishing Company, Inc.. p. 310.ISBN 978-1-4027-5796-9. Retrieved 2011-02-05.
27. ^ Batty, Michael (1985-04-04). "Fractals - Geometry Between Dimensions". New Scientist (Holborn Publishing Group) 105(1450): 31.
28. ^ Russ, John C. (1994). Fractal surfaces. 1. Springer. p. 1.ISBN 978-0-306-44702-0. Retrieved 2011-02-05.
29. ^ Edgar, Gerald (2008). Measure, topology, and fractal geometry. New York, NY: Springer-Verlag. p. 1. ISBN 978-0-387-74748-4.
30. ^ Karperien, Audrey (2004).http://www.webcitation.org/65DyLbmF1 Defining microglial morphology: Form, Function, and Fractal Dimension. Charles Sturt University. Retrieved 2012-02-05.
31. ^ Spencer, John; Thomas, Michael S. C.; McClelland, James L. (2009). Toward a unified theory of development : connectionism and dynamic systems theory re-considered. Oxford/New York: Oxford University Press. ISBN 978-0-19-530059-8.
32. ^ Frame, Angus (3 August 1998). "Iterated Function Systems". In Pickover, Clifford A.. Chaos and fractals: a computer graphical journey : ten year compilation of advanced research. Elsevier. pp. 349–351. ISBN 978-0-444-50002-1. Retrieved 4 February 2012.
33. ^ "Haferman Carpet". WolframAlpha. Retrieved 18 October 2012.
34. ^ ^a b c d Hahn, Horst K.; Georg, Manfred; Peitgen, Heinz-Otto (2005). "Fractal aspects of three-dimensional vascular constructive optimization". In Losa, Gabriele A.; Nonnenmacher, Theo F.. Fractals in biology and medicine. Springer. pp. 55–66. ISBN 978-3-7643-7172-2.>
35. ^ Fathallah-Shaykh, Hassan M. (2011). "Fractal Dimension of the Drosophila Circadian Clock". Fractals 19 (4): 423–430.doi:10.1142/S0218348X11005476. edit
36. ^ "Hunting the Hidden Dimension." Nova. PBS. WPMB-Maryland. 28 October 2008.
37. ^ Sornette, Didier (2004). Critical phenomena in natural sciences: chaos, fractals, selforganization, and disorder : concepts and tools. Springer. pp. 128–140. ISBN 978-3-540-40754-6.
38. ^ Meyer, Yves; Roques, Sylvie (1993). Progress in wavelet analysis and applications: proceedings of the International Conference "Wavelets and Applications," Toulouse, France - June 1992. Atlantica Séguier Frontières. p. 25. ISBN 978-2-86332-130-0. Retrieved 2011-02-05.
39. ^ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw (2000). Pattern formation in biology, vision and dynamics. World Scientific. p. 78. ISBN 978-981-02-3792-9.
40. ^ Addison, Paul S. (1997). Fractals and chaos: an illustrated course. CRC Press. pp. 44–46. ISBN 978-0-7503-0400-9. Retrieved 2011-02-05.
41. ^ Pincus, David (September 2009). "The Chaotic Life: Fractal Brains Fractal Thoughts". psychologytoday.com.
42. ^ Frame, Michael; and Mandelbrot, Benoît B.; A Panorama of Fractals and Their Uses
43. ^ Nelson, Bryn; Sophisticated Mathematics Behind African Village Designs Fractal patterns use repetition on large, small scale, San Francisco Chronicle, Wednesday, February 23, 2009
44. ^ Hohlfeld, Robert G.; Cohen, Nathan (1999). "Self-similarity and the geometric requirements for frequency independence in Antennae". Fractals 7 (1): 79–84.doi:10.1142/S0218348X99000098.
45. ^ Reiner, Richard; Waltereit, Patrick; Benkhelifa, Fouad; Müller, Stefan; Walcher, Herbert; Wagner, Sandrine; Quay, Rüdiger; Schlechtweg, Michael et al. (2012). "Fractal structures for low-resistance large area AlGaN/GaN power transistors".Proceedings of ISPSD: 341.doi:10.1109/ISPSD.2012.6229091. ISBN 978-1-4577-1596-9.
46. ^ Chen, Yanguang (2011). "Modeling Fractal Structure of City-Size Distributions Using Correlation Functions". PLoS ONE 6(9): e24791. doi:10.1371/journal.pone.0024791.PMC 3176775. PMID 21949753. edit
47. ^ "Applications". Retrieved 2007-10-21.
48. ^ Smith, Robert F.; Mohr, David N.; Torres, Vicente E.; Offord, Kenneth P.; Melton III, L. Joseph (1989). "Renal insufficiency in community patients with mild asymptomatic microhematuria".Mayo Clinic proceedings. Mayo Clinic 64 (4): 409–414.PMID 2716356. edit
49. ^ Landini, Gabriel (2011). "Fractals in microscopy". Journal of Microscopy 241 (1): 1–8. doi:10.1111/j.1365-2818.2010.03454.x. PMID 21118245. edit
50. ^ Cheng, Qiuming (1997). "Multifractal Modeling and Lacunarity Analysis". Mathematical Geology 29 (7): 919–932.doi:10.1023/A:1022355723781. edit
51. ^ Chen, Yanguang (2011). "Modeling Fractal Structure of City-Size Distributions Using Correlation Functions". PLoS ONE 6(9): e24791. doi:10.1371/journal.pone.0024791.PMC 3176775. PMID 21949753. edit
52. ^ Burkle-Elizondo, Gerardo; Valdéz-Cepeda, Ricardo David (2006). "Fractal analysis of Mesoamerican pyramids". Nonlinear dynamics, psychology, and life sciences 10 (1): 105–122.PMID 16393505. edit
53. ^ Brown, Clifford T.; Witschey, Walter R. T.; Liebovitch, Larry S. (2005). "The Broken Past: Fractals in Archaeology". Journal of Archaeological Method and Theory 12: 37. doi:10.1007/s10816-005-2396-6. edit
54. ^ Saeedi, Panteha; Sorensen, Soren A.. "An Algorithmic Approach to Generate After-disaster Test Fields for Search and Rescue Agents". Proceedings of the World Congress on Engineering 2009: 93–98. ISBN 978-988-17-0125-1.
55. ^ Brams, Steven J.; MacLennan, Bruce J.; Täuber, Uwe C.; Manzan, Sebastiano; Mizrach, Bruce; Petkova, Ralitsa; Haas, Markus; Pigorsch, Christian et al. (2009). "Fractal Geometry, A Brief Introduction to". Encyclopedia of Complexity and Systems Science. pp. 3700. doi:10.1007/978-0-387-30440-3_218. ISBN 978-0-387-75888-6. edit

[edit]Further reading

• Barnsley, Michael F., and Rising, Hawley; Fractals Everywhere. Boston: Academic Press Professional, 1993. ISBN 0-12-079061-0
• Falconer, Kenneth; Techniques in Fractal Geometry. John Wiley and Sons, 1997. ISBN 0-471-92287-0
• Jürgens, Hartmut; Peitgen, Heins-Otto; and Saupe, Dietmar; Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, 1992. ISBN 0-387-97903-4
• Mandelbrot, Benoît B.; The Fractal Geometry of Nature. New York: W. H. Freeman and Co., 1982. ISBN 0-7167-1186-9
• Peitgen, Heinz-Otto; and Saupe, Dietmar; eds.; The Science of Fractal Images. New York: Springer-Verlag, 1988. ISBN 0-387-96608-0
• Pickover, Clifford A.; ed.; Chaos and Fractals: A Computer Graphical Journey - A 10 Year Compilation of Advanced Research. Elsevier, 1998. ISBN 0-444-50002-2
• Jones, Jesse; Fractals for the Macintosh, Waite Group Press, Corte Madera, CA, 1993. ISBN 1-878739-46-8.
• Lauwerier, Hans; Fractals: Endlessly Repeated Geometrical Figures, Translated by Sophia Gill-Hoffstadt, Princeton University Press, Princeton NJ, 1991. ISBN 0-691-08551-X, cloth. ISBN 0-691-02445-6 paperback. "This book has been written for a wide audience..." Includes sample BASIC programs in an appendix.
• Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 0-19-850839-5 and ISBN 978-0-19-850839-7.
• Wahl, Bernt; Van Roy, Peter; Larsen, Michael; and Kampman, Eric; Exploring Fractals on the Macintosh, Addison Wesley, 1995.ISBN 0-201-62630-6
• Lesmoir-Gordon, Nigel; "The Colours of Infinity: The Beauty, The Power and the Sense of Fractals." ISBN 1-904555-05-5 (The book comes with a related DVD of the Arthur C. Clarke documentary introduction to the fractal concept and the Mandelbrot set.
• Liu, Huajie; Fractal Art, Changsha: Hunan Science and Technology Press, 1997, ISBN 9787535722348.
• Gouyet, Jean-François; Physics and Fractal Structures (Foreword by B. Mandelbrot); Masson, 1996. ISBN 2-225-85130-1, and New York: Springer-Verlag, 1996. ISBN 978-0-387-94153-0. Out-of-print. Available in PDF version at."Physics and Fractal Structures"(in (French)). Jfgouyet.fr. Retrieved 2010-10-17.
• Bunde, Armin; Havlin, Shlomo (1996). Fractals and Disordered Systems. Springer.
• Bunde, Armin; Havlin, Shlomo (1995). Fractals in Science. Springer.
• ben-Avraham, Daniel; Havlin, Shlomo (2000). Diffusion and Reactions in Fractals and Disordered Systems. Cambridge University Press.

[edit]External links

Wikimedia Commons has media related to: Fractal

Wikibooks has a book on the topic of: Fractals

• Fractals at the Open Directory Project
• Scaling and Fractals presented by Shlomo Havlin, Bar-Ilan University
• Hunting the Hidden Dimension, PBS NOVA, first aired August 24, 2011
• Benoit Mandelbrot: Fractals and the Art of Roughness, TED (conference), February 2010

[hide] v   t   e Fractals Characteristics Fractal dimension (Hausdorff dimension & Topological dimension)   Self-similarity   Recursion Iterated function system Koch snowflake   Cantor set   Sierpinski carpet   Sierpinski triangle   Space-filling curve   Dragon curve T-square   Menger sponge Strange attractor Multifractal system L-system Space-filling curve Escape-time fractals Mandelbrot set   Julia set   Burning Ship fractal   Nova fractal   Lyapunov fractal Random fractals Lévy flight   Percolation theory   Self-avoiding walk   Fractal landscape   Brownian motion   Brownian tree Diffusion-limited aggregation People Georg Cantor   Felix Hausdorff   Gaston Julia   Paul Pierre Lévy   Aleksandr Lyapunov   Benoît Mandelbrot Lewis Fry Richardson   Wacław Sierpiński   Helge von Koch Other List of fractals by Hausdorff dimension "How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension"